Материал помещен в архив. Актуальный материал по теме см. здесь

ОПТИМИЗАЦИЯ РАЗМЕРА ЗАКАЗА МАТЕРИАЛЬНЫХ ЗАПАСОВ ПРИ МНОГОПРОДУКТОВЫХ ПОСТАВКАХ

На практике при управлении материальными запасами широкой товарной номенклатуры организации нередко необходимо прибегать к многопродуктовым поставкам, т.е. поставкам, которые предусматривают доставку в одном транспортном средстве нескольких наименований товаров.

Очевиден вопрос: какое влияние оказывает многопродуктовая поставка на размеры заказов отдельных наименований товаров, формирующих данную поставку?

В логистике запасов известность получила зависимость по определению оптимального размера заказа (формула (1)):

где q₀ - оптимальный размер заказа по конкретному наименованию материальных запасов (товару), шт. (т, куб.м, рулонов, бухт);

C^e_o - транспортные и связанные с ними расходы (оформление документов, погрузка, разгрузка) на выполнение 1 заказа по данному наименованию товара, тыс.руб.;

S - величина спроса (потребления) данного наименования товара за установленный промежуток времени, шт./кв. (шт./мес., шт./год);

С^e_xp - издержки на хранение единицы (1 шт., т и т.д.) товара в течение периода времени потребления величины (S), тыс.руб./(шт. х кв.) (тыс.руб./(шт. х год) и т.д.);

Е - коэффициент эффективности финансовых вложений за период времени потребления величины (S);

P - цена за единицу товара, тыс.руб./шт. (тыс.руб./т и т.д.).

Оптимальный размер заказа товара - размер заказа, при котором совокупные издержки (Сс) при формировании и управлении запасами (расходы на покупку, доставку и хранение данного наименования товара, а также затраты, связанные с замораживанием денежных средств, вложенных в создание запасов) принимают минимальное значение (формула (2)):

где С_о - транспортные и связанные с ними расходы (оформление документов, погрузка, разгрузка) по данному наименованию товара за период времени потребления величины (S), тыс.руб./кв. (тыс.руб./год и т.д.);

С_хр - издержки на хранение данного наименования товара в течение периода времени потребления величины (S), тыс.руб./кв. (тыс.руб./год и т.д.).

Коэффициент (Е), который оценивает эффективность финансовых вложений за период времени потребления величины (S), может варьироваться в следующих пределах.

1. Минимальный размер коэффициента (Е), обусловливающий максимальные размеры заказов, устанавливается в случае наличия в организации достаточного количества свободных денежных (оборотных) средств и должен составлять величину, соответствующую депозитному проценту за период времени потребления величины (S). Например, анализируемый период - 1 месяц. Следовательно, депозитный процент за месяц при 12-процентном годовом составит 1 %. В этом случае коэффициент (Е) равен 0,01 за 1 месяц (1 % / 100 %).

2. Максимальный размер коэффициента (Е) устанавливается в случае отсутствия в организации свободных денежных средств или ее интенсивного развития. Это, в свою очередь, обусловливает минимальные размеры заказов, что позволяет высвободить максимальное количество денежных (оборотных) средств для финансирования, например, оплаты труда и т.п. Его величина определяется в зависимости от источника свободных денежных средств.

2.1. Свободные денежные средства формируются за счет привлечения кредитных ресурсов банков. В этом случае размер коэффициента (Е) должен составлять величину, соответствующую годовой процентной ставке по банковскому кредиту за период времени потребления величины (S), согласно формуле (3):

где CK - годовая процентная ставка по банковскому кредиту, %;

n - количество повторений в течение года установленного промежутка времени (анализируемого периода), за которое потребляется величина (S).

2.2. Свободные денежные средства формируются за счет собственных резервов организации. В этом случае величину коэффициента в соответствии с выбранным анализируемым периодом необходимо определять по формуле (4):

где R - достигнутый среднегодовой уровень рентабельности готовой продукции в организации или рентабельности продаж в торговле, %;

N_об - количество оборотов в течение года, которые совершают оборотные средства (денежные средства, необходимые для производства и реализации продукции, участвующей в одном кругообороте).

Например, достигнутый среднегодовой уровень рентабельности продукции в организации составляет 12 %; анализируемый период - 1 месяц; количество оборотов готовой продукции (оборотных средств) в течение года - 12 оборотов. Следовательно, в данном случае коэффициент (Е), в отличие от первого пункта, равен 0,12 за 1 месяц, т.е. в большинстве случаев (для производственных организаций) минимальная величина коэффициента (Е) отличается от максимального значения на порядок (в 10 раз).

Важно подчеркнуть, что в торговых организациях минимальная величина коэффициента (Е) может отличаться от максимального значения на 2 порядка (в 100 раз).

Следовательно, численное значение коэффициента (Е) устанавливается с учетом финансового состояния организации-потребителя. Другими словами, финансовое состояние организации влияет на величину размера заказа. Так, если организация имеет сложное финансовое положение, коэффициент (Е) должен принимать максимальное или близкое к нему значение. При этом, как отмечалось выше, будут получены минимальные размеры заказа, т.е. финансовое состояние организации не позволяет делать крупные заказы. И наоборот, если организация отличается абсолютной финансовой устойчивостью, коэффициент (Е) должен принимать минимальное или близкое к нему значение. При этом будут получены максимальные размеры заказа, т.е. такое финансовое состояние организации позволяет делать большие заказы.

Важно подчеркнуть, что такие составляющие формулы (1), как издержки на хранение единицы товара (C^e_xp), коэффициент эффективности финансовых вложений (E) должны быть привязаны к временному интервалу, за который потребляется величина (S). Так, например, если величина потребления или сбыта (S) определенного наименования товара рассматривается за квартал, то и величины (C^e_xp) и (E) должны рассчитываться за квартал.

Следует также указать на ограничения применения формулы (1) по определению оптимального размера заказа:

• первым и наиболее весомым ограничением применения формулы (1) будет оптимизация размера заказа при имеющих место оптовых скидках. Данное обстоятельство обусловлено, во-первых, тем, что при ее выводе не учитывалась зависимость затрат на закупку (произведение величины потребления (S) на цену (Р) за единицу товара) от размера заказа. Во-вторых, тем, что затраты на закупку имеют в подавляющем большинстве производственных ситуаций наибольшее значение по сравнению с другими статьями прямых затрат, связанных с управлением запасами;

• второе ограничение применения формулы, которое носит сугубо математический характер: при ее выводе предусматривалось, что транспортные и связанные с ними расходы на выполнение 1 заказа (C^e_o) не зависят от размера заказа (постоянны). Однако на самом деле параметр (C^e_o) зависит от размера заказа, но эта зависимость, как правило, оказывает лишь косвенное влияние на величину и характер изменения совокупных издержек (С_о) по доставке товара в течение периода времени, за которое потребляется величина (S). Между тем данное обстоятельство указывает на необходимость дополнительных научных изысканий;

• третье ограничение представляет собой условие применения формулы, которое заключается в том, что издержки (C^e_xp) на хранение единицы товара в течение периода времени потребления величины (S) не должны зависеть от размера заказа. Это достигается в случае эффективного использования площади складского помещения. Так, например, если на площади в 1 кв.м может храниться 3 т товара, то эту возможность необходимо использовать на 80-100 %;

• при определении максимального значения коэффициента (E) по формуле (3) желательно принимать среднее значение количества оборотов (N_об), которые совершают оборотные средства в течение года. В противном случае, если показатель (N_об) пересчитывать с учетом коэффициента оборачиваемости по каждому наименованию запасов, коэффициент (E) будет напрямую зависеть от размера заказа, что неправомерно с математической точки зрения. Другими словами, при применении формулы (1) для соответствующей производственной задачи коэффициент (E) должен иметь постоянное значение независимо от размера заказа.

Оптимальный размер заказа можно определить также, используя графический метод, который основан на нахождении точки минимума графической зависимости совокупных издержек при формировании запасов (рисунок 1).

Рисунок 1

Графический метод определения оптимального размера заказа

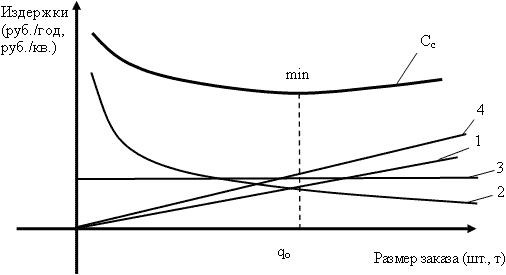Для этого необходимо сложить:

• график 1 издержек на хранение (С_хр), которые изменяются прямо пропорционально размеру заказа;

• график 2 издержек на транспортные расходы (C^e_о х S / q), который имеет для большинства производственных ситуаций гиперболическую форму (обратно пропорциональную зависимость);

• график 3 издержек, связанных с закупкой товара (P х S), который представляет собой горизонтальную прямую, так как данные расходы не зависят от размера заказа, если нет оптовых скидок.

Расчет оптимального размера заказа материальных запасов при многопродуктовых поставках рассмотрим на примере следующей производственной ситуации.

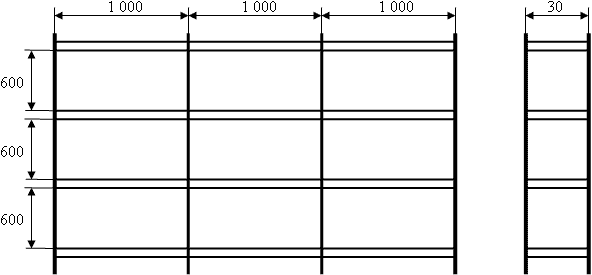
Пример Организация осуществляет розничную и мелкооптовую торговлю бумагой офисной формата А4 в пачках по 500 листов. Пачки бумаги доставляются и хранятся в коробках, вмещающих 5 пачек. Закупочная цена - 45,0 тыс.руб. за 1 пачку при размере заказа до 200 пачек, 40,0 тыс.руб. за 1 пачку при размере заказа от 200 пачек. Среднемесячное потребление бумаги - 1 000 пачек. Габаритные размеры коробки - длина х ширина х высота - 300 х 220 х 275 мм. Масса брутто 1 коробки - 12,5 кг. Коробки хранятся на полках стеллажа СТ-031 (рисунок 2). Максимальная нагрузка на полку стеллажа - 200 кг. Издержки, связанные с эксплуатацией 1 кв.м арендуемого склада в течение месяца, составляют 50,0 тыс.руб.   Рисунок 2   Размеры стеллажа СТ-031

Закупки бумаги осуществляются у поставщика, удаленность которого от организации составляет 40 км. Доставка обеспечивается собственными транспортными средствами грузоподъемностью 1 000, 2 000 и 3 000 кг, тарифные ставки на внутрихозяйственные грузоперевозки для которых составляют соответственно 1,5, 2,2 и 2,5 тыс.руб./км. Доставка бумаги может производиться параллельно с другими видами товарной продукции. Рентабельность продаж в организации составляет в среднем 15,0 %. В этой связи организация не нуждается в свободных денежных средствах.

Несмотря на то что производственная задача предусматривает наличие оптовой скидки, определим оптимальный размер заказа бумаги по формуле (1). При этом если полученный размер заказа (как уже отмечалось) будет находиться в пределах действия оптовой скидки (более 200 пачек), то это решение экономически целесообразно.

Условие производственной задачи также предусматривает, что доставка бумаги может производиться параллельно с другими видами товарной продукции (многопродуктовая поставка).

В результате анализа формулы (2) было установлено, что при заказе товара у 1 поставщика (с 1 склада) параллельно с другими видами необходимой продукции до полной загрузки транспортного средства с уменьшением размера заказа товара сокращаются также и совокупные издержки (С_с). Другими словами, чем меньше размер заказа, тем лучше это с экономической точки зрения. Данный факт обусловлен тем, что при заказе товара у одного поставщика параллельно с другими видами необходимой продукции до полной загрузки транспортного средства издержки (С_о) (см. формулу (2)) по доставке товара в течение периода времени, за которое потребляется величина (S), будут иметь постоянную величину независимо от размера заказа (рисунок 3).

Рисунок 3

Графики издержек, связанных с формированием и управлением запасами, от размера заказа при поставке товара со склада одного поставщика параллельно с другими видами необходимой продукции до полной загрузки транспортного средства

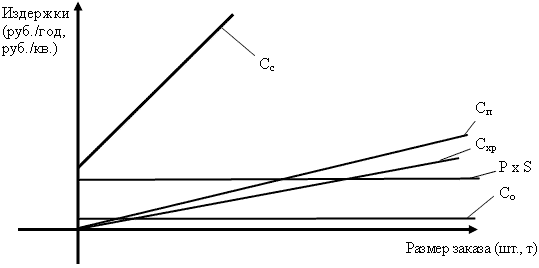Однако данная ситуация на практике встречается крайне редко, так как лишь в отдельных случаях 1 поставщик способен обеспечить поставку по всей номенклатуре производственных запасов. В этой связи, чтобы обеспечить полную загрузку транспортного средства в соответствии с его грузоподъемностью, требуется прибегать к услугам, как правило, 2 и более поставщиков, что в результате вызывает рост затрат на выполнение 1 заказа (С_о), а их зависимость от размера заказа будет носить традиционный (гиперболический) характер.

Более того, размер заказа не может стремиться к нулю, так как он в большинстве производственных ситуаций должен быть больше величины потребления товара за время выполнения заказа.

Принимая во внимание относительно незначительное расстояние транспортировки, интуитивно устанавливаем размер заказа на уровне 100 пачек (20 коробок). Масса заказа 250 кг (12,5 кг / 1 коробка х 20 коробок) требует применить транспортное средство грузоподъемностью 1 000 кг. При этом предусматривается, что параллельно с бумагой у поставщика будет заказываться другой товар. Допустим, его масса будет также равна 250 кг. Следовательно, расходы на транспортировку бумаги в структуре совокупных транспортных затрат будут занимать 50 %.

Во-первых, определим транспортные расходы на выполнение 1 заказа (C^e_o) по доставке бумаги. Издержки на выполнение 1 заказа на расстояние 80 км (туда и обратно) составят 60,0 тыс.руб. (50 % / 100 % х 80 км х 1,5 тыс.руб./км).

Во-вторых, определим издержки на хранение 1 пачки бумаги в течение месяца (C^e_xp). Так как при стеллажном размещении товаров затраты на хранение единицы запасов (C^e_xp) не зависят от размера заказа, расчет данных затрат целесообразно производить не с учетом интуитивного размера заказа, а руководствуясь количеством товара, который вмещается на 1 полке стеллажа. Линейные размеры 1 полки (ячейки) стеллажа СТ-031 позволяют разместить на ней 8 коробок бумаги, или 40 пачек в коробках. Принимая во внимание рисунок 2, можно утверждать, что 1 полка стеллажа занимает лишь 0,075 кв.м пола склада (3 м х 0,3 м / 12 полок), а с учетом проходов и проездов не более 0,1 кв.м. Следовательно, издержки на хранение 1 пачки бумаги (C^e_xp) за месяц составят 0,25 тыс.руб. (0,1 кв.м х 50,0 тыс.руб./(мес. x кв.м) х 1 мес. / 20 пачек), где 20 пачек - это среднее количество пачек бумаги на 1 полке стеллажа в течение месяца (q / 2 = 40 / 2).

Так как организация не нуждается в свободных денежных средствах (нормальное финансовое состояние), принимаем величину коэффициента эффективности финансовых вложений (Е) за период времени, равный 1 месяцу, на уровне близком к минимальному значению - 0,05. Тогда размер заказа согласно формуле (1) составит:

Q₀ = √2 х 60 х 1 000 / (0,25 + 0,05 х 45,0) = 219 пачек.

Полученный расчетный размер заказа (219 пачек) позволяет утверждать, что принятый интуитивно размер заказа на уровне 100 пачек имеет значительное отличие от оптимальной величины.

В этой связи осуществляем второе приближение. Для этого устанавливаем размер заказа с определенным опережением к уровню 219 пачек, принимая в качестве второго приближения размер заказа, равный 250 пачек, или 50 коробок. Масса заказа 625 кг (12,5 кг / 1 коробка х 50 коробок) требует применить транспортное средство грузоподъемностью 1 000 кг. При этом также предполагается, что параллельно с бумагой у поставщика будет заказан другой товар. Допустим, его масса (как в первом случае) будет равна 250 кг. Следовательно, расходы на транспортировку бумаги в структуре совокупных транспортных затрат будут занимать 71,4 % (625 / (625 + 250) х 100 %).

Определим транспортные расходы на выполнение 1 заказа (C^e_o) по доставке бумаги. Издержки на выполнение 1 заказа на расстояние 80 км (туда и обратно) составят 85,68 тыс.руб. (71,4 % / 100 % х 80 км х 1,5 тыс.руб./км).

Издержки на хранение 1 пачки бумаги в течение месяца (C^e_xp) останутся прежними (0,25 тыс.руб.).

Тогда размер заказа согласно формуле (1) с учетом оптовой скидки составит:

Q₀ = √2 х 85,68 х 1 000 / (0,25 + 0,05 х 40,0) = 276 пачек.

Полученный расчетный оптимальный размер заказа (276 пачек) отличается на 10,4 % от размера заказа, принятого в качестве второго приближения, что допустимо для подобного рода расчетов. Более того, его величина находится в пределах действия оптовой скидки. Следовательно, оптимальный размер заказа бумаги при заданных исходных данных и условии, что бумага будет доставляться параллельно с другими видами товаров, составляет около 250 пачек, или 50 коробок.

Рассчитаем размер заказа для ситуации, когда бумага доставляется отдельно от других товаров. В данном случае вся величина транспортных расходов на выполнение 1 заказа (C^e_o) будет приходиться на затраты, связанные с формированием и управлением запасами бумаги. Их величина составит 120,0 тыс.руб. (2 х 40 км х 1,5 тыс.руб./км).

Тогда размер заказа согласно формуле (1) составит:

Q₀ = √2 х 120 х 1 000 / (0,25 + 0,05 х 40,0) = 327 пачек.

Таким образом, полученные результаты позволяют утверждать, что доставка определенного наименования товара параллельно с другими товарами посредством применения транспортных средств большой и особо большой грузоподъемности позволяет сократить размер заказа данного наименования товара по сравнению с ситуацией, когда товар доставляется отдельно от других видов продукции. При этом сокращение размера заказа данного наименования товара должно находиться в пределах величины его потребления за время выполнения заказа.

26.11.2013

Петр Дроздов, кандидат экономических наук, доцент Института бизнеса и менеджмента технологий Белорусского государственного университета