Материал помещен в архив

ОПТИМИЗАЦИЯ СЕТЕВЫХ МОДЕЛЕЙ ПО КРИТЕРИЮ «ВРЕМЯ - ЗАТРАТЫ»

Методика оптимизации сетевых моделей по критерию «Время - затраты»

Оптимизацию по критерию «Время - затраты» проводят с целью сократить срок выполнения проекта в целом. Такая оптимизация имеет смысл только в том случае, когда время выполнения работ может быть уменьшено за счет задействования дополнительных ресурсов, что приводит к повышению затрат на выполнение работ (схема 1).

Введем следующие обозначения:

- Сн(i, j) - стоимость выполнения работы (i, j), имеющей нормальную продолжительность Тн(i, j);

- Ту(i, j) - время ускоренного выполнения работы (i, j);

- Сп(i, j) - повышенную стоимость выполнения работы (i, j), имеющей ускоренную продолжительность;

- Ск - ежедневные косвенные затраты организации, выполняющей проект;

- С₀ - ограничение по средствам, выделенным на проведение оптимизации;

- Спр - сумма прямых затрат на выполнение всего проекта.

Для оценки величины дополнительных затрат, связанных с ускорением выполнения той или иной работы, используют либо нормативы, либо данные о выполнении аналогичных работ в прошлом. Под параметрами работ Сн(i, j) и Сп(i, j) понимаются так называемые прямые затраты, непосредственно связанные с выполнением конкретной работы.

Схема 1

Зависимость прямых затрат на работу от времени ее выполнения

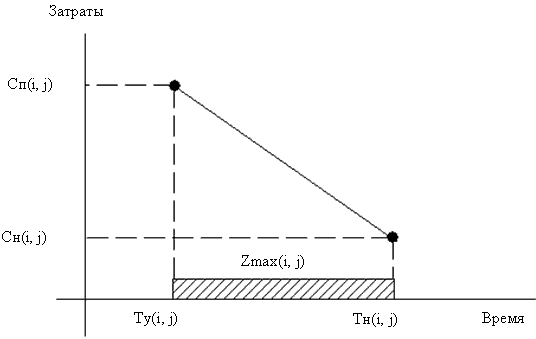Таким образом, косвенные затраты типа административно-управленческих в процессе сокращения длительности проекта во внимание не принимаются, однако их влияние учитывается при выборе окончательного календарного плана проекта.

Важные параметры работы (i, j) при проведении данного вида оптимизации:

- коэффициент нарастания затрат (формула (1)):

который показывает затраты денежных средств, необходимые для сокращения длительности работы (i, j) на один день;

- запас времени для сокращения длительности работы в текущий момент времени (формула (2)):

где tт(i, j) - длительность работы (i, j) на текущий момент времени, максимально возможное значение запаса времени работы равно (формула (3)):

Эта ситуация имеет место, когда длительность работы (i, j) еще ни разу не сокращали, т.е. tт(i, j) = Тн(i, j).

Общая схема проведения оптимизации «Время - затраты»

1. Исходя из нормальных длительностей работ Тн(i, j) определяются критические Lкр и подкритические Lп пути сетевой модели и их длительности Ткр и Тп.

2. Определяется сумма прямых затрат на выполнение всего проекта С⁰пр при нормальной продолжительности работ.

3. Рассматривается возможность сокращения продолжительности проекта, для чего анализируются параметры критических работ проекта.

Для сокращения выбирается критическая работа с min коэффициентом нарастания затрат k(i, j), имеющая ненулевой запас времени сокращения Zт(i, j).

Время Δt(i, j), на которое необходимо сжать длительность работы (i, j), определяется по формуле (4):

где ΔТ = Ткр - Тп - разность между длительностью критического и подкритического путей в сетевой модели. Необходимость учета параметра ΔТ вызвана нецелесообразностью сокращения критического пути более чем на ΔТ единиц времени. В этом случае критический путь перестанет быть таковым, а подкритический путь, наоборот, станет критическим, т.е. длительность проекта в целом принципиально не может быть сокращена больше чем на ΔТ.

4. В результате сжатия критической работы временные параметры сетевой модели изменяются, что может привести к появлению других критических и подкритических путей. Вследствие удорожания ускоренной работы общая стоимость проекта Спр увеличивается на величину ΔСпр (формула (5)):

5. Для измененной сетевой модели определяются новые критические и подкритические пути и их длительности, после чего необходимо продолжить оптимизацию с шага 3. Ограничение в денежных средствах, их исчерпание - причина окончания оптимизации. Если не учитывать подобное ограничение, оптимизацию можно продолжать до тех пор, пока у работ, которые могли бы быть выбраны для сокращения, не будет исчерпан запас времени сокращения.

Обратите внимание!

Рассмотренная общая схема оптимизации предполагает наличие одного критического пути в сетевой модели. В случае существования нескольких критических путей необходимо либо сокращать общую для них всех работу, либо одновременно сокращать несколько различных работ, принадлежащих различным критическим путям. Возможна комбинация данных вариантов. В каждом случае критерием выбора работы или работ для сокращения должен служить минимум затрат на их общее сокращение.

Проведение оптимизации сетевой модели по критерию «Время - затраты»

Максимально возможное уменьшение сроков выполнения проекта при минимально возможных дополнительных затратах для следующих исходных данных представим в таблице 1, на схеме 2.

Схема 2

Исходная сетевая модель

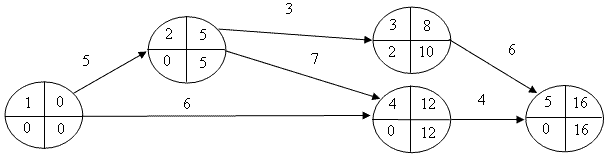Исходя из нормальных длительностей работ получаем следующие характеристики сетевой модели:

- длительность проекта Т⁰кр = 16 дней;

- критический путь L⁰кр = 1,2,4,5 или L⁰кр = (1, 2); (2, 4); (4, 5);

- подкритический путь L⁰кр = 1, 2, 3, 5 или L⁰кр = (1, 2); (2, 3); (3, 5), Т⁰п = 14 дней.

Кроме того, вычислим коэффициенты нарастания затрат и максимальные запасы времени сокращения работ сетевой модели (таблица 2).

Шаг 1. Для сокращения выбираем критическую работу (4, 5) с минимальным коэффициентом k(4, 5) = 1,0 руб./день. Текущий запас сокращения времени работы (4, 5) на данном шаге равен Z⁰т(4, 5) = Zmax(4, 5) = 3 дня. Разность между продолжительностью критического и подкритического путей равна 2 дня: ΔT⁰ = Т⁰кр - Т⁰п. Поэтому согласно описанной выше общей схеме оптимизации сокращаем работу (4, 5) на 2 дня: Δt¹ = min(3, 2). Новая текущая длительность работы: t¹т(4, 5) = 4 - 2 = 2 дня, а запас ее дальнейшего сокращения уменьшается до 1 дня: Z¹т(4, 5). Измененный сетевой график представлен на схеме 3.

Схема 3

Сетевая модель после первого шага оптимизации

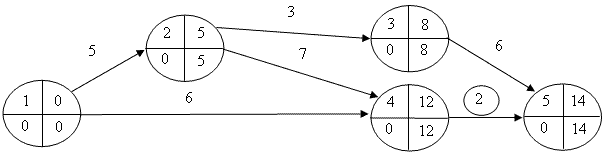После ускорения работы (4, 5) возникли следующие изменения:

- затраты на работу (4, 5) возросли на 2,0 руб.: 1,0 руб./день х 2 дня и общие затраты на проект составили: С¹пр = 44,0 + 2,0 = 46,0 руб.;

- длительность проекта Т¹кр = 14 дней;

- критические пути L¹кр = 1, 2, 3, 5 и L¹кр = 1, 2, 4, 5;

- подкритический путь L¹п = 1,4,5, Т¹п = 8 дней.

Шаг 2. Одновременное сокращение двух критических путей можно провести, либо ускорив работу (1, 2), принадлежащую обоим путям, либо одновременно ускорив различные работы из каждого пути. Наиболее дешевый вариант - ускорение работ (3, 5) и (4, 5) - 1,6 руб./день за обе работы, тогда как ускорение работы (1, 2) обошлось бы в 7,0 руб./день. Поскольку ΔТ¹ = Т¹кр - Т¹п = 6, то сокращаем работы (3, 5) и (4, 5) на 1 день: Δt² = min(5, 1, 6). Запасы дальнейшего сокращения времени работ сокращаются до 0 дней: Z²т(3, 5) = 4 и Z²т(4, 5) = 0. Измененный сетевой график представлен на схеме 4.

Схема 4

Сетевая модель после второго шага оптимизации

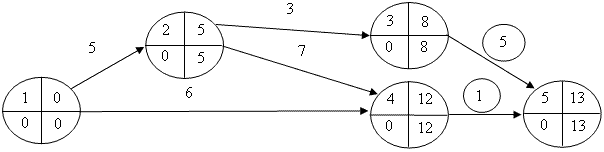После ускорения работ (3, 5) и (4, 5) возникли следующие изменения:

- общие затраты на проект составили: С²пр = 46,0 + 0,6 х 1 + 1,0 х 1 = 47,6 руб.;

- длительность проекта: Т²кр = 13 дней;

- два критических пути: L²кр = 1, 2, 3, 5 и L²кр = 1, 2, 4, 5;

- подкритический путь: L²п = 1, 4, 5, Т²п = 7 дней.

Шаг 3. Поскольку на данном шаге работа (4, 5) исчерпала свой запас ускорения, то наиболее дешевым вариантом сокращения обоих критических путей является ускорение работ (3, 5) и (2, 4) - 2,6 руб./день за обе работы. Сокращаем работы (3, 5) и (2, 4) на Δt³ = min(4, 4, 6) = 4 дня. Запасы дальнейшего сокращения времени работ (3, 5) и (2, 4) обнуляются. Измененный сетевой график представлен на схеме 5:

Схема 5

Сетевая модель после третьего шага оптимизации

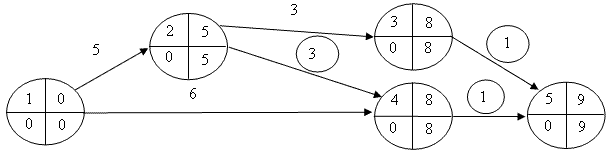После ускорения работ (3, 5) и (2, 4) возникли следующие изменения:

- общие затраты на проект составили С³пр = 47,6 + 0,6 х 4 + 2,0 х 4 = 58,0 руб.;

- длительность проекта Т³кр = 9 дней;

- два критических пути L³кр = 1, 2, 3, 5 и L³кр = 1, 2, 4, 5;

- подкритический путь L³п = 1, 4, 5, Т³п = 7 дней.

Шаг 4. Поскольку, кроме работы (1, 2), все остальные работы критического пути L³кр = 1, 2, 4, 5 исчерпали свой запас времени ускорения, единственно возможным вариантом сокращения обоих критических путей является ускорение работы (1, 2). Сокращаем работу (1, 2) на 2 дня: Δt⁴ = min(2, 2).

Запас дальнейшего сокращения времени работы (1, 2) обнуляется. Измененный сетевой график представлен на схеме 6.

Схема 6

Сетевая модель после четвертого шага оптимизации

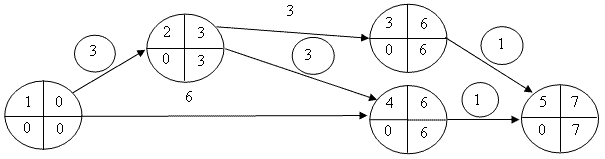После ускорения работы (1, 2) возникли следующие изменения:

- общие затраты на проект составили С⁴пр = 58,0 + 7,0 х 2 = 72,0 руб.;

- длительность проекта Т⁴кр = 7 дней;

- три критических пути L⁴кр = 1, 2, 3, 5, L⁴кр = 1, 2, 4, 5 и L⁴кр = 1, 4, 5.

Подкритические пути отсутствуют.

Дальнейшая оптимизация стала невозможной, поскольку все работы критического пути L⁴кр = 1, 2, 4, 5 исчерпали свой запас времени ускорения, а значит, проект не может быть выполнен меньше чем за 7 дней: Т⁴кр = 7.

Таким образом, при отсутствии ограничений на затраты минимально возможная длительность проекта составляет 7 дней. Сокращение длительности проекта с 16 до 7 дней потребовало 28,0 руб. прямых затрат. В отличие от прямых затрат при уменьшении продолжительности проекта косвенные затраты (Ск = 1,5 руб./день) убывают, что показано на схеме 7.

Схема 7

Время - затраты

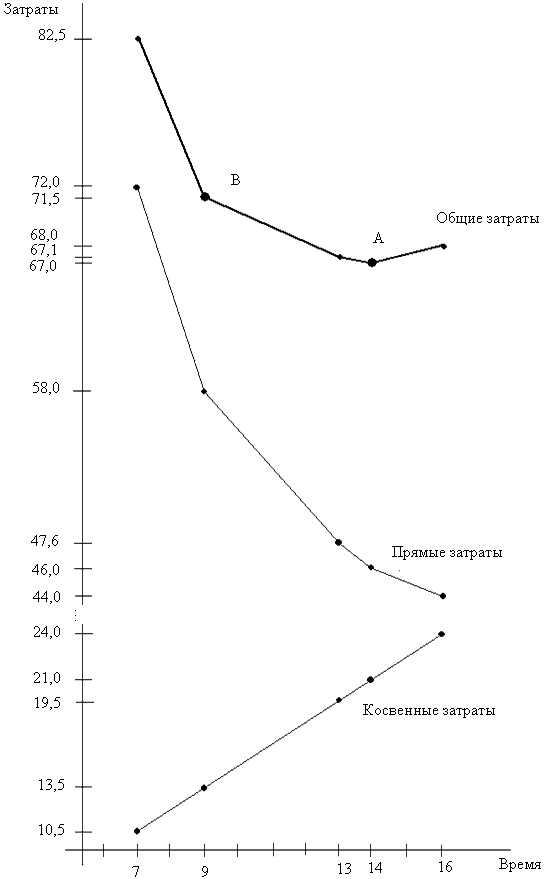31.08.2011 г.

Татьяна Алесинская, кандидат технических наук, доцент кафедры менеджмента Таганрогского технологического института Южного федерального университета