Материал помещен в архив. Актуальный материал по теме см. здесь

ВЫБИРАЕМ ОПТИМАЛЬНЫЙ РАДИУС ОБСЛУЖИВАНИЯ РАСПРЕДЕЛИТЕЛЬНОГО ЦЕНТРА

Согласно общеизвестному определению распределительный центр представляет собой склад, с которого идут отгрузки на другие склады товаропроводящей сети организации. При этом распределительный центр закупает товары от организаций-производителей или организаций оптовой торговли (которые, например, находятся в других регионах страны или за границей) и распределяет их более мелкими партиями заказчикам (организациям-потребителям мелкооптовой и розничной торговли) через свою или их товаропроводящую сеть (схема 1).

В круг основных задач распределительного центра, как правило, входят:

• централизованный заказ (как правило, крупными партиями) согласно суммарным потребностям мелкооптовой и розничной торговли товаропроводящей сети;

• разгрузка, приемка и размещение товара на складе;

• хранение товара;

• комплектование заказов, предусматривающее при необходимости переформирование поступивших на склад укрупненных грузовых единиц, упаковку, штрихкодирование, стикеровку товара;

• отгрузка и доставка;

• в отдельных случаях сертификация и таможенное оформление товара и др.

Как показывает практика товаропроводящих сетей, в некоторых случаях организация имеет в зоне обслуживания 2 распределительных центра и более. В этой связи правомерен вопрос: какие точки розничной торговли должны обслуживаться соответствующим распределительным центром? Другими словами, какой оптимальный радиус обслуживания соответствующего распределительного центра?

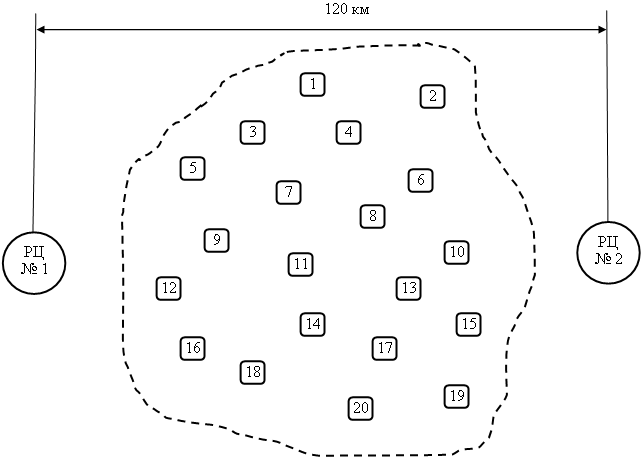
Например, в зоне потребления действует 2 распределительных центра, призванных обслуживать 20 точек розничной торговли (схема 2). Известно, что расстояние между ними составляет 120 км. Необходимо определить, какие точки розничной торговли должны обслуживаться соответствующим распределительным центром.

Схема 2

Размещение распределительных центров в зоне обслуживания

Принимая во внимание определение понятия «распределительный центр», издержки точки розничной торговли, связанные с формированием и управлением товарными запасами за установленный промежуток времени (например, месяц), не будут включать затраты, связанные с покупкой товара, и потери из-за «замораживания» денежных средств, вложенных в создание запасов. Данный факт обусловлен тем, что магазины не закупают товар у распределительного центра, а просто получают его в соответствии с величиной спроса.

Следовательно, величина издержек точек розничной торговли (С^м_с) за установленный промежуток времени будет включать транспортные расходы, связанные с доставкой товара, и затраты на хранение (формула (1)):

где S - величина спроса (потребления) данного наименования товара в соответствующей точке розничной торговли за установленный промежуток времени, шт./мес. (шт./кв-л, шт./год);

С_о - совокупные издержки по доставке товара в течение периода времени, за которое потребляется величина (S) для соответствующей точки розничной торговли, тыс.руб./мес. (тыс.руб./кв-л, тыс.руб./год);

С_хр - издержки на хранение товара в соответствующей точке розничной торговли в течение периода времени, за которое потребляется величина (S), тыс.руб./мес. (тыс.руб./кв-л, тыс.руб./год);

С^е_о - транспортные и связанные с ними расходы (оформление документов, погрузка, разгрузка и т.д.) на выполнение одного заказа по данному наименованию товара для соответствующей точки розничной торговли, тыс.руб.;

q - размер заказа соответствующей точки розничной торговли у соответствующего распределительного центра по данному наименованию материальных запасов (товара), шт. (т, куб.м, рулонов, бухт);

C^e_xp - издержки на хранение единицы (1 шт., 1 т и т.д.) товара в соответствующей точке розничной торговли в течение периода времени потребления величины (S), тыс.руб./(шт. х мес.) (тыс.руб./(шт. х кв-л), тыс.руб./(шт. х год) и т.д.).

Предварительный анализ зависимости (1) позволяет сделать следующие выводы.

1. Издержки на хранение (С_хр) в соответствующей точке розничной торговли зависят лишь от размера заказа (q), так как издержки на хранение единицы конкретного наименования товара (C^e_хр) - величина постоянная. При этом размер заказа (q) прямо пропорционален удаленности распределительного центра. Другими словами, чем ближе находится распределительный центр к точке розничной торговли, тем меньше будут издержки (С_хр). Следовательно, издержки (С_хр) не оказывают влияния на ответ об оптимальном радиусе обслуживания распределительного центра.

2. Исходя из первого вывода, ответ на вопрос о том, какой распределительный центр должен обслуживать соответствующую точку розничной торговли, следует искать в сравнении совокупных издержек по доставке товара (С_о). При этом важно учитывать, как осуществляется доставка товара. На практике возможны следующие варианты:

• доставка обеспечивается транспортными средствами распределительных центров;

• доставка обеспечивается транспортными средствами точек розничной торговли;

• доставка осуществляется с использованием маятниковых маршрутов с обратным холостым пробегом;

• доставка осуществляется с использованием кольцевых развозочных маршрутов.

Если доставка осуществляется транспортным средством соответствующей точки розничной торговли с фиксированным размером тарифной ставкой за 1 км транспортировки, то в этом случае, как и с издержками (С_хр), предпочтение в обслуживании следует отдавать тому распределительному центру, который находится ближе.

В случае если доставка обеспечивается транспортными средствами распределительных центров, ответ на вопрос об оптимальном радиусе обслуживания зависит от того, как обеспечивается доставка: с использованием маятниковых или кольцевых маршрутов.

Рассмотрим первую ситуацию: доставка обеспечивается транспортными средствами распределительных центров с использованием маятниковых маршрутов (с обратным холостым пробегом).

Очевидно, что в этом случае радиусы обслуживания соответствующих распределительных центров можно найти, принимая во внимание следующее равенство (формула (2)):

где R₁, R₂ - радиусы обслуживания соответственно распределительных центров № 1 и № 2;

T₁, T₂ - тарифные ставки за 1 км транспортировки соответственно распределительных центров № 1 и № 2.

Анализ формулы (2) позволяет утверждать, что радиусы обслуживания соответствующих распределительных центров будут соотноситься между собой так же, как соотносятся тарифные ставки за 1 км транспортировки соответствующих распределительных центров (формула (3)):

Например, если тарифные ставки за 1 км транспортировки соответствующих распределительных центров равны между собой, то и радиусы обслуживания будут равны между собой. Для нашей производственной задачи (схема 2) радиусы составят 60 км (120 / 2).

Рассмотрим вторую ситуацию: доставка обеспечивается транспортными средствами распределительных центров с использованием кольцевых развозочных маршрутов.

Для данной ситуации применение понятия «оптимальный радиус обслуживания распределительного центра» неправомерно, так как ответ на вопрос о том, какой распределительный центр должен обслуживать соответствующую точку розничной торговли, зависит не только от ее удаленности и тарифных ставок на транспортировку, но и от развитости дорожной инфраструктуры, числа и потребностей других точек розничной торговли, обслуживание которых будет вестись на соответствующем кольцевом развозочном маршруте. Поэтому применим алгоритм решения транспортных задач в сетевой форме без ограничения пропускной способности сети.

Общий алгоритм

Общий алгоритм решения подобных задач рассмотрим на следующем примере. На схеме 3 изображена транспортная сеть. При этом числовые значения в скобках со знаком «-» означают потребности соответствующих пунктов (точек розничной торговли); в свою очередь, со знаком «+» - наличие товаров на складах распределительных центров.

Схема 3

Транспортная сеть

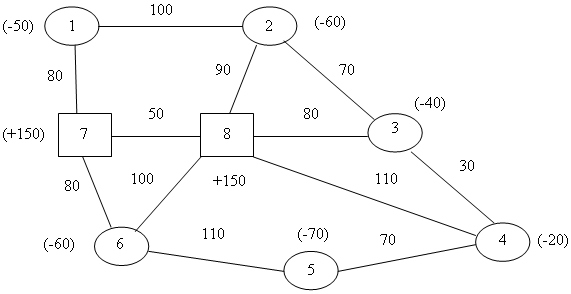Шаг 1. Проверяем главное условие равенства ресурсов поставщиков и спроса потребителей. Условие выполняется. Следовательно, можем приступать к решению задачи.

Шаг 2. Составляем исходный план, при котором ресурсы поставщиков должны быть отправлены, а спрос потребителей удовлетворен (стрелками на схеме 4 показаны направления грузопотоков, а числами - количество перевозимой продукции).

Схема 4

Исходный план распределения ресурсов

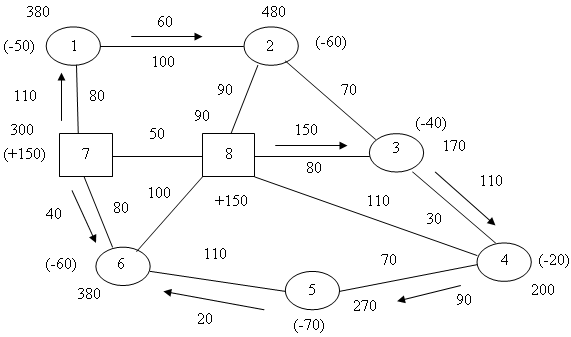Шаг 3. Присваиваем потенциалы вершинам так, чтобы впоследствии не иметь дело с отрицательными числами. Например, вершине 7 потенциал равный 300. Назначаем потенциалы остальным вершинам, придерживаясь следующего правила: при движении по дугам сети в направлении следования грузопотока к потенциалу предыдущей вершины прибавляем длину дуги, а при движении по дугам против потока эту длину из потенциала предыдущей вершины вычитаем (см. схему 4).

Следует отметить, что в случае, если невозможно назначить потенциалы всем вершинам относительно одной заданной (в нашем случае вершина 7), транспортная сеть разбивается на отдельные (независимые) части, оптимизация которых возможна или с применением метода оптимизации кольцевых маршрутов, или в виде сетевой модели.

Шаг 4. Проверяем выполнение условия оптимальности для всех дуг сети, на которых нет грузопотока, т.е. соблюдение следующего выражения (формула (4)):

где Р_j - потенциал в j-м пункте (стоимость у потребителя);

L_i - потенциал в i-м пункте (стоимость у поставщика);

С_ij - расстояние между пунктами (стоимость транспортировки).

Такими дугами (парами пунктов) будут: 2-3 (480 - 170 = 310 > 70); 7-8 (300 - 90 = 210 > 50); 4-8 (200 - 90 = 110 = 110); 6-8 (380 - 90 = 290 > 100); 2-8 (480 - 90 = 390 > 90). Условие оптимальности нарушено на 4 дугах из 5, следовательно, исходный план не оптимален.

Шаг 5. Выбираем дугу 2-8 с максимальным нарушением условия оптимальности и направляем по ней грузопоток от вершины с меньшим потенциалом (8) до вершины с большим потенциалом (2). Далее необходимо составить замкнутый контур, состоящий из дуг с потоком и выбранной дуги с нарушением. Это можно сделать единственным способом, составив контур из дуг 8-2, 2-1, 1-7, 7-6, 6-5, 5-4, 4-3, 3-8. Продвигаясь по данному контуру от точки 8 к точке 2 и далее к точке 8, находим наименьший встречный поток (20). Прибавляя это число ко всем попутным грузопотокам и вычитая его из всех встречных, получаем улучшенный вариант перевозок (схема 5).

Схема 5

Первый улучшенный вариант распределения ресурсов

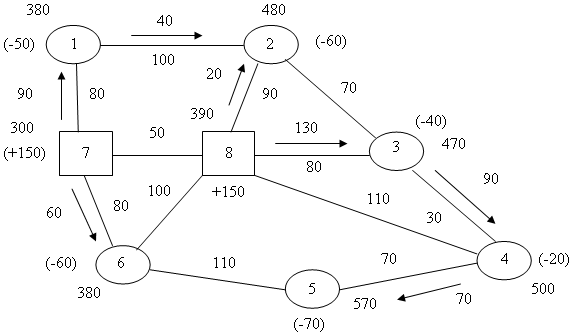Повторяем шаг 3. Нет необходимости заново подсчитывать все потенциалы вершин сети, достаточно исправить лишь потенциалы тех вершин, в которых изменилось направление грузопотоков.

Шаг 6. Опять проверяем выполнение условия оптимальности для всех дуг сети, на которых нет грузопотока: 2-3 (480 - 470 = 10 < 70); 8-7 (390 - 300 = 90 > 50); 8-6 (390 - 380 = 10 < 100); 5-6 (570 - 380 = 190 > 110); 4-8 (500 - 390 = 110 = 110). Условие не выполняется на 2 из 5 дуг. При этом наибольшее нарушение на дуге 5-6. Повторяя шаг 5, получаем второй улучшенный план распределения ресурсов (схема 6).

Схема 6

Второй улучшенный вариант распределения ресурсов

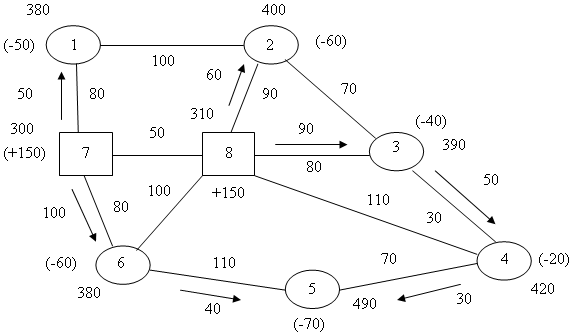Шаг 7. Снова проверяем выполнение условия оптимальности для всех дуг сети, на которых нет грузопотока: 2-1 (400 - 380 = 20 < 100); 2-3 (400 - 390 = 10 < 70); 4-8 (420 - 310 = 110 = 110); 6-8 (380 - 310 = 70 < 100); 8-7 (310 - 300 = 10 < 50). На всех дугах условие оптимальности выполняется, следовательно, второй улучшенный план распределения ресурсов оптимален.

Сравнивая исходный и второй улучшенный планы распределения ресурсов по показателю совокупной транспортной работы, получаем то, что в результате оптимизации совокупная транспортная работа (транспортные расходы) уменьшилась (уменьшились) на 22 %.

Выводы

Анализ полученных результатов позволяет сделать следующие выводы:

1. При обслуживании точек розничной торговли предпочтение следует отдавать тем распределительным центрам, которые находятся ближе. Исключение составляют ситуации, когда доставка товара осуществляется транспортными средствами распределительных центров.

2. Для производственных ситуаций, когда доставка обеспечивается транспортными средствами распределительных центров с использованием маятниковых маршрутов (с обратным холостым пробегом), радиусы обслуживания соответствующих распределительных центров будут соотноситься между собой так же, как соотносятся тарифные ставки за 1 км транспортировки соответствующих распределительных центров.

3. Для производственных ситуаций, когда доставка обеспечивается транспортными средствами распределительных центров с использованием кольцевых развозочных маршрутов, ответ на вопрос о том, какой распределительный центр должен обслуживать соответствующую точку розничной торговли, можно найти путем применения алгоритма решения транспортных задач в сетевой форме без ограничения пропускной способности сети.

13.08.2013

Петр Дроздов, кандидат экономических наук, доцент Белорусского государственного аграрного технического университета