Оптимизация размера заказа материальных запасов при различных способах укладки на складе 30.03.2012 автор Дроздов П.

Расчет от 30.03.2012
Автор: Дроздов П.

Оптимизация размера заказа материальных запасов при различных способах укладки на складе

Искать как словосочетание

Искать в документе Искать в содержании

0/0

Материал помещен в архив

ОПТИМИЗАЦИЯ РАЗМЕРА ЗАКАЗА МАТЕРИАЛЬНЫХ ЗАПАСОВ ПРИ РАЗЛИЧНЫХ СПОСОБАХ УКЛАДКИ НА СКЛАДЕ

Введение

Материальные запасы или продукция, ожидающая потребления, составляют значительную часть оборотных средств организации. Поэтому нерациональное управление запасами, например, на производственном предприятии, или приводит к «затормаживанию» оборачиваемости денежного капитала, вложенного в создание запасов, или может сорвать выполнение производственной программы, а также привести к ее изменению.

Материальные запасы, являющиеся наименее ликвидными краткосрочными активами, представляют собой по сути «замороженные» денежные средства.

Между тем некоторые менеджеры, опасаясь возможной нехватки товаров, а также при значительных административных издержках систематически создают избыточные запасы в целях подстраховки и во избежание «головной боли».

Однако большинство организаций малого и среднего бизнеса избегают больших запасов с низкой оборачиваемостью, что позволяет увеличить оборачиваемость запасов, а также сократить издержки на их содержание.

Как свидетельствует практика, величина материальных запасов, хранящихся на складах, во многом зависит от размера заказываемых партий по отдельным наименованиям товаров. В свою очередь размер заказа материальных запасов зависит от способа их укладки (хранения) на складе.

В связи с этим проблема определения оптимального размера заказа материальных запасов при различных способах укладки на складе актуальна и имеет важное практическое значение.

Определение оптимального размера заказа

В логистике запасов широкую известность получила зависимость по определению оптимального размера заказа, названная в честь ученого, ее представившего, - формула Уилсона (1934 г.).

При ее выводе ученый исходил из условия идеальной системы управления запасами, суть которой заключается в том, что доставка нового заказа осуществляется в момент, когда предыдущий полностью закончился, тем самым устанавливая средний размер запаса (остатка) товара на складе на уровне половины величины заказываемой партии. Так, если размер одной заказываемой и доставляемой партии равен q, то средняя величина запаса товара на складе составит q / 2 ((q + 0) / 2).

При этом ученым учитывались затраты, связанные с приобретением товара, его доставкой и хранением. Так, например, за определенный период времени объем оборота (потребления или сбыта) определенного наименования товара составляет S. Тогда затраты на приобретение товара представляют собой произведение величины S на цену за единицу товара Р. Установив транспортные и связанные с ними расходы на выполнение одного заказа на уровне С^е_о, совокупные издержки (С_о) по доставке товара в течение периода времени, за которое потребляется величина S, ученый предложил определять по формуле (1):

С_о = С^е_о х S / q.

(1)

При этом отношение S / q показывает, какое количество заказов будет сделано за период времени потребления величины S.

Аналогично установив тариф на хранение единицы запасов в течение периода времени, за которое потребляется величина S в размере С^е_хр, ученый предложил следующую зависимость по определению затрат на хранение (С_хр) (см. формулу (2)):

С_хр = С^е_хр х q / 2.

(2)

Таким образом, было получено основное уравнение по определению совокупных издержек (С_с) при формировании и управлении запасами за установленный период времени потребления величины S (см. формулу (3)):

С_с = P х S + C^e_o х S / q + С^е_хр х q / 2.

(3)

Следовательно, оптимальный размер заказа товара - это такой размер заказа, при котором совокупные издержки (С_с) при формировании и управлении запасами принимают минимальное значение.

Очевидно, оптимальный размер заказа будет достигнут, когда совокупные издержки принимают минимальное значение или когда первая производная уравнения по размеру заказа будет равна нулю (см. формулу (4)):

С_с' = С^е_хр / 2 - C^e_o х S / q² = 0.

(4)

Оптимальный размер заказа (q_о) определяется по формуле (5):

	______________
	q_о = √2 х C^e_o х S / С^е_хр,	(5)

где q_о - оптимальный размер заказа по конкретному наименованию материальных запасов (товару), шт. (т, куб.м, рулонов, бухт и т.д.);

C^e_o - транспортные и связанные с ними расходы (оформление документов, погрузка, разгрузка) на выполнение одного заказа по данному наименованию товара, тыс.руб.;

S - величина спроса (потребления) данного наименования товара за установленный промежуток времени, шт./кв. (шт./мес., шт./год);

С^е_хр - издержки на хранение единицы (одной штуки, тонны и т.д.) товара в течение периода времени потребления величины S, тыс.руб./(шт./кв.) (тыс.руб./(шт./год) и т.д.).

Между тем, анализируя порядок вывода формулы Уилсона (5), а также саму формулу, можно утверждать, что она не учитывает потери («замораживание») финансового капитала, вложенного в создание запасов, или, другими словами, потери, обусловленные затормаживанием оборачиваемости вложенных в запасы денежных средств.

Так, применение формулы для различных по стоимости материалов (например, листовой стали обычного качества и высоколегированной), цены на которые могут отличаться в несколько раз, при одинаковых исходных данных даст один и тот же результат. Очевидно, это неправомерно с экономической точки зрения.

Поэтому для того, чтобы сократить влияние негативного эффекта (замораживание денежного капитала, вложенного в создание запасов), совокупные издержки при формировании запасов должны дополнительно включать расходы, обусловленные потерями от недополучения дохода (С_п). Величину этих потерь за период времени потребления величины S рекомендуется определять по формуле (6):

С_п = Е х q / 2 х P,

(6)

где Е - коэффициент эффективности финансовых вложений за период времени потребления величины S, 1/кв. (1/год, 1/мес.).

Коэффициент Е отражает, какая доля суммы денежных средств (Р х q / 2), которая в среднем имеет место на складе, «замораживается» при создании запасов за период времени потребления величины S.

Таким образом, величина С_п имеет двойственную экономическую природу: с одной стороны, она оценивает размер потерь, обусловленных вложением финансовых средств в создание запасов («замораживание»), а с другой - устанавливает величину дополнительного дохода, который можно было бы получить в случае отказа от создания запасов. Так, например, финансовые средства, необходимые для создания среднего запаса (q / 2), в размере P х q / 2 можно было, как минимум, положить в банк и получать доход по депозиту или вложить в дальнейшее развитие организации с целью увеличения доходов в перспективе. По причине двойственной природы величину С_п не включают в структуру прямых производственных затрат (при бухгалтерском учете). Однако при проведении расчетов по сравнительной экономической эффективности или при бизнес-планировании учет данной величины должен быть обязательным.

Коэффициент Е, который оценивает эффективность финансовых вложений за период времени потребления величины S, может варьировать в следующих пределах:

1) минимальный размер должен составлять величину, соответствующую депозитному проценту за период времени потребления величины S. Так, например, анализируемый период - один месяц. Следовательно, депозитный процент за месяц при 12-процентном годовом составит 1 %. В этом случае коэффициент Е равен 0,01 за один месяц (1 % / 100 %).

Максимальный размер определяется достигнутым уровнем рентабельности готовой продукции в организации и устанавливается в случае интенсивного развития организации (бывает крайне редко). Его величину в соответствии с выбранным анализируемым периодом необходимо определять по формуле (7):

Е = R / (n х 100 %) х N_об,

(7)

где R - достигнутый среднегодовой уровень рентабельности готовой продукции в организации, %;

n - количество установленных промежутков времени (анализируемых периодов), за которое потребляется величина S, в течение года;

N_об - количество оборотов готовой продукции (оборотных средств) в течение года.

Например, достигнутый среднегодовой уровень рентабельности продукции в организации составляет 12 %; анализируемый период - один месяц; количество оборотов готовой продукции (оборотных средств) в течение года - 12 оборотов. Следовательно, в данном случае коэффициент Е, в отличие от первого пункта, равен 0,12 за один месяц. Иначе говоря, в большинстве случаев минимальная величина коэффициента Е отличается от максимальной на порядок (в 10 раз).

Таким образом, формула по определению оптимального размера заказа с учетом потерь от недополучения дохода (С_п) в отличие от формулы Уилсона будет иметь следующий вид (см. формулу (8)):

	_____________________
	q_o = √2 х C^e_o х S / (С^е_хр +E х P),	(8)

P - цена за единицу товара, тыс.руб./шт. (тыс.руб./т и т.д.).

Необходимо обратить внимание, что такие составляющие формулы (8), как издержки на хранение единицы товара (С^е_хр), а также коэффициент эффективности финансовых вложений (E) должны быть привязаны к временному интервалу, за который потребляется величина S. Так, например, если величина потребления или сбыта определенного наименования товара S рассматривается за квартал, то и величины С^е_хр и E должны рассчитываться за квартал.

Как следует из опыта хозяйственной деятельности, на практике редко применяют формулу по определению оптимального размера заказа, объясняя это или скорее оправдывая тем, что спрос (потребление) на товар с течением времени постоянно меняется. Однако на самом деле такое положение вещей вызвано простым неумением применять данную зависимость на практике. Так, например, оптимальный размер заказа может быть рассчитан (в случае необходимости) для различных интервалов времени (месяц, декада, неделя и даже один день).

Примеры оптимизации размера заказа при различных способах укладки на складе

Расчет оптимального размера заказа стали листовой при штабельном размещении запасов рассмотрим на примере следующей производственной ситуации.

Пример 1

Агросервисная организация планирует производство рабочих органов сельскохозяйственных машин. При этом известно, что в соответствии с технологией изготовления будет использоваться листовая сталь с линейными размерами 6 000х1 500х10 мм стоимостью 8 100 тыс.руб. за 1 т (по состоянию на 1 января 2012 г). Удаленность поставщика стали - 750 км. В соответствии с прогнозной годовой программой производства рабочих органов сельскохозяйственных машин потребуется 100 т листовой стали в год. При этом исходя из проведенных маркетинговых исследований (возможных каналов сбыта готовой товарной продукции) планируемое потребление стали в разрезе по месяцам года представлено в таблице 1.

Таблица 1

Планируемое потребление листовой стали по месяцам года

т
Ян-варь	Фев-раль	Март	Ап-рель	Май	Июнь	Июль	Ав-густ	Сен-тябрь	Ок-тябрь	Но-ябрь	Де-кабрь
6	12	15	10	6	5	8	15	10	5	4	4

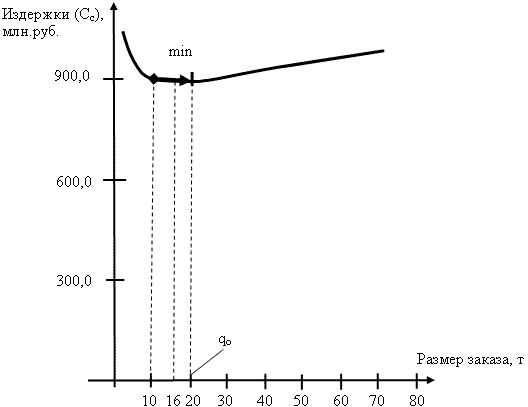
Также известно, что допустимая нагрузка на 1 кв.м пола для склада по хранению стали составляет 4 т/кв.м. Издержки по содержанию 1 кв.м за месяц - 21,0 тыс.руб. (собственное помещение). В результате письменных переговоров с торговым домом установлено, что время выполнения одного заказа составит 30 календарных дней.

Рассчитаем оптимальный размер заказа листовой стали по формуле (8).

Так как транспортные расходы на выполнение одного заказа (C^e_o), а также затраты на хранение одной тонны стали (С^е_хр) зависят от размера заказа, который еще предстоит определить, необходимо в качестве первого приближения интуитивно установить размер заказа.

Принимаем размер заказа на уровне 10 т, тем самым предполагая, что для транспортировки будет использоваться автотранспорт.

Во-первых, определим транспортные расходы на выполнение одного заказа (C^e_o) по доставке листовой стали из г.Москвы. По состоянию на 1 января 2012 г. величина тарифной ставки на оказание автотранспортных услуг для автотранспортного агрегата грузоподъемностью 10 т составляла в среднем 4,5 тыс.руб. за 1 км. Следовательно, издержки на выполнение одного заказа из г.Москвы (1 500 км туда и обратно) составят 6 750 тыс.руб. (1 500 км х 4,5 тыс.руб./км).

Во-вторых, определим издержки на хранение 1 т стали в течение года (С^е_хр). С учетом линейных размеров стального листа (6 000 х 1 500 мм), допустимой нагрузки на 1 кв.м пола для складов по хранению стали (4 т/кв.м), а также ширины проходов и проездов минимально необходимая площадь хранения должна составлять 15 кв.м. Рассчитаем издержки на хранение 1 т (С^е_хр) за год. Они составят 756,0 тыс.руб. (15 кв.м х 21,0 тыс.руб. / (мес. х кв.м) х 12 мес. / 5 т), где 5 т - это среднее количество стали (средний остаток), которое будет иметь место на складе (q / 2 = 10 / 2).

Принимая величину коэффициента эффективности финансовых вложений (Е) за период времени, равный одному году, на уровне 0,5 (т.е. предполагая возможность дальнейшего наращивания производственной программы новых изделий), определим размер заказа согласно формуле (8):

q_o = √2 х 6 750 х 100 / (756,0 + 0,5 х 8 100) = 16,8 т.

Полученный расчетный размер заказа (16,8 т) позволяет утверждать, что принятый интуитивно размер заказа на уровне 10 т имеет значительное отличие от оптимальной величины.

В связи с этим осуществляем второе приближение. Для этого устанавливаем размер заказа с определенным опережением к уровню 16,8 т, принимая размер заказа равным 20 т.

Уточняем транспортные расходы на выполнение одного заказа (C^e_o) по доставке листовой стали из г.Москвы. По состоянию на 1 января 2012 г. величина тарифной ставки на оказание автотранспортных услуг для автотранспортного агрегата грузоподъемностью 20 т составляла в среднем 5,7 тыс.руб. за 1 км. Следовательно, издержки на выполнение одного заказа из г.Москвы (1 500 км туда и обратно) будут равны 8 550 тыс.руб. (1 500 км х 5,7 тыс.руб./км).

Уточняем издержки на хранение 1 т стали в течение года (С^е_хр). Они составят 378,0 тыс.руб. (15 кв.м х 21,0 тыс.руб./(мес. х кв.м) х 12 мес. / 10 т), где 10 т - это среднее количество стали (средний остаток), которое будет иметь место на складе (q / 2 = 20 / 2).

Уточняем размер заказа согласно формуле (8):

q_o = √2 х 8 550 х 100 / (378,0 + 0,5 х 8 100) = 19,7 ≈ 20,1 т.

Так как принятый размер заказа согласно второму приближению (20,0 т) практически не отличается от оптимальной величины (19,7 т), следовательно, окончательно устанавливаем размер заказа на уровне 20,0 т, или 29 листов (с учетом того что масса 1 листа равна 0,702 т).

На рисунке 1 представлен график, отражающий зависимость издержек, связанных с формированием и управлением запасами листовой стали, от размера заказа с учетом потерь денежных ресурсов, вложенных в создание запасов затрат (С_п), согласно формуле (9):

С_с = P х S + C^e_o х S / q + С^е_хр х q / 2 + E х q / 2 х P.

(9)

Рисунок 1

Зависимость издержек, связанных с формированием и управлением запасами листовой стали, от размера заказа

Рассчитаем оптимальный размер заказа листовой стали по формуле Уилсона с учетом исходных данных и того, что ее доставка предположительно будет осуществляться автотранспортом:

q_о = √2 х 8 550 х 100 / 378,0 = 67,3 т.

Полученный размер оптимального размера заказа согласно формуле Уилсона позволяет утверждать, что доставка листовой стали должна осуществляться не автомобильным, а железнодорожным транспортом, так как максимальный размер одной партии поставки автомобильным транспортом ограничивается грузоподъемностью автотранспортного агрегата (фуры), которая обычно не превышает 25 т.

В свою очередь минимальная площадь склада, занимаемая сталью, должна составлять уже не 15 кв.м, а не менее 30 кв.м. Это объясняется тем, что на 9 кв.м площади пола, которую занимает один стальной лист (6 000 х 1 500 мм) с учетом допустимой нагрузки на 1 кв.м (4 т/кв.м), максимально можно хранить не более 36 т стали. На этом основании, чтобы разместить 67,3 т стали с учетом ширины проходов и проездов, потребуется не 15, а 30 кв.м площади склада.

Уточним оптимальный размер заказа по формуле Уилсона. Во-первых, пересчитаем транспортные расходы на выполнение одного заказа (C^e_o) по доставке листовой стали. По состоянию на 1 января 2012 г. величина тарифной ставки на оказание услуг железнодорожного транспорта составляла в среднем 30,0 тыс.руб. за 1 ваг.-км. При этом в отличие от автотранспорта расчет ведется только в одну сторону (750 км). Следовательно, издержки на выполнение одного заказа с учетом того, что потребуется один вагон, составят 22 500 тыс.руб. (1 вагон х 750 км х 30,0 тыс.руб./ваг.-км).

Во-вторых, пересчитаем издержки на хранение 1 т стали в течение года (С^е_хр). Они составят 189,0 тыс.руб. (30 кв.м х 21,0 тыс.руб./(мес. х кв.м) х 12 мес. / 40 т), где 40 т - это предполагаемое среднее количество стали, которое будет иметь место на складе.

В таком случае уточненный размер заказа согласно формуле Уилсона составит:

q_о = √2 х 22 500 х 100 / 189,0 = 154,3 т.

Уточненный согласно формуле Уилсона размер заказа (154,3 т) отличается от исходного (67,3 т) в 2,3 раза.

В связи с этим осуществляем второе приближение. Для этого устанавливаем размер заказа с определенным опережением к уровню 154,3 т, принимая размер заказа равным 3 вагонам, или 235 т. При этом для хранения стали потребуется 7 штабелей.

Издержки на выполнение одного заказа с учетом того, что потребуются 3 вагона, составят 67 500,0 тыс.руб. (3 вагона х 750 км х 30,0 тыс.руб./ваг.-км).

Издержки на хранение 1 т стали в течение года (С^е_хр) составят 220,5 тыс.руб. (105 кв.м х 21,0 тыс.руб./(мес. х кв.м) х 12 мес. / 120 т), где 120 т - это предполагаемое среднее количество стали, которое будет иметь место на складе.

Тогда уточненный размер заказа согласно формуле Уилсона составит:

q_о = √2 х 67 000 х 100 / 220,5 = 246,5 т.

Расчетный размер заказа (246,5 т) отличается от принятого (235,0 т) на 5,0 %, что допустимо для подобного рода расчетов.

Такой значительный размер заказа стали (235 т - 245 т, или 3 вагона), с одной стороны, «заморозит» значительные финансовые ресурсы на длительный срок (более одного года). С другой стороны, данный размер заказа, как свидетельствует практика, способно обеспечить лишь крупное промышленное предприятие (например, открытое акционерное общество «МАЗ» или республиканское унитарное предприятие «МТЗ»), имеющее соответствующие финансовые возможности.

Из анализа полученных результатов следует, что оптимальный размер заказа согласно формуле (8) в 12 раз меньше по сравнению с размером заказа согласно формуле Уилсона.

Определим размер годового экономического эффекта по формуле (10):

Э = С_с1 - С_с2,

(10)

где С_с1 - совокупные годовые издержки на формирование и управление запасами при размере заказа, рассчитанном согласно формуле Уилсона, тыс.руб.;

С_с2 - совокупные годовые издержки на формирование и управление запасами при размере заказа, рассчитанном согласно формуле (8), тыс.руб.

Определим совокупные годовые издержки на формирование и управление запасами с учетом потерь, обусловленных «замораживанием» финансовых средств, вложенных в создание запасов, при размере заказа, рассчитанном согласно формуле Уилсона:

С_с1 = 8 100 х 100 + 67 500 х 100 / 235 + 220,5 х 235 / 2 + 0,5 х 235 / 2 х 8 100 = 134 507,2 тыс.руб.

Определим совокупные годовые издержки на формирование и управление запасами при размере заказа, рассчитанном согласно формуле (8):

С_с2 = 8 100 х 100 + 8 550 х 100 / 20 + 378,0 х 20 / 2 + 0,5 х 20 / 2 х 8 100 = 897 030,0 тыс.руб.

В этом случае величина годового экономического эффекта при формировании и управлении запасами при размере заказа, рассчитанном согласно формуле (8), составит:

Э = С_с1 - С_с2 = 134 507,2 - 897 030,0 = 443 477,2 тыс.руб.

Следовательно, формирование материальных запасов путем осуществления заказов по отдельным наименованиям товаров в размерах, рассчитанных согласно формуле (8), в отличие от формулы Уилсона позволит получать значительный экономический эффект в результате ускорения оборачиваемости финансового капитала, вкладываемого в создание запасов, а также сокращения издержек, связанных с хранением товаров.

Однако при небольших расстояниях транспортировки (доставки) товара и относительно высоких издержках на хранение единицы товара (С^е_хр) размер заказа, рассчитанный по формуле (8), может иметь незначительную величину. В подобных ситуациях размер заказа следует увеличить с учетом ожидаемого потребления товара за время выполнения заказа.

Так, для нашего примера ожидаемое потребление за время выполнения заказа (30 дней, см. исходные данные) составляет 12 т (0,4 т / день х 30 дней), где 0,4 т - величина среднего дневного потребления листовой стали за год (100 т / 250 раб. дней / год). Следовательно, размер заказа можно оставить на уровне расчетного (20 т), так как его размер превышает ожидаемое потребление листовой стали за время выполнения заказа (20 > 12).

Полученный оптимальный размер заказа (20 т) был рассчитан исходя из годового потребления стали (100 т/год). Однако важно определить, как меняется размер заказа, если в качестве временного интервала принимается другая величина, например, месяц.

Опираясь на данные таблицы 1, можно утверждать, что в течение года наблюдаются серьезные колебания потребления листовой стали. Так, например, потребление за март почти в 4 раза превышает потребление за декабрь. Возникает вопрос: будет ли наблюдаться аналогичное колебание размера заказа, если в качестве временного интервала выступает календарный месяц?

Рассчитаем оптимальный размер заказа по формуле (8), принимая временной интервал, равный одному месяцу, на примере мая.

Величина потребления листовой стали за май составляет 6 т (S = 6 т) (см. таблицу 1). Транспортные расходы на выполнение одного заказа (C^e_o) оставляем на прежнем уровне (C^e_o = 8 550 тыс.руб.). В свою очередь издержки на хранение 1 т стали (С^е_хр) должны быть привязаны к временному интервалу (1 месяц), т.е. должны быть пересчитаны. С учетом ранее проведенного расчета они составят 31,5 тыс.руб. (15 кв.м х 21,0 тыс.руб./(мес. х кв.м) х 1 мес. / 10 т), где 10 т - это предполагаемое среднее количество стали, которое будет иметь место на складе (q / 2). По этой же причине должен быть пересмотрен и коэффициент эффективности финансовых вложений (E). Так, за год его величина составляла 0,5, следовательно, за месяц он будет равен 0,042 (0,5 / 12).

В данном случае оптимальный размер заказа согласно формуле (8) составит:

q_о = √2 х 8 550 х 6 / (31,5 + 0,042 х 8 100) = 16,6 т.

Пересчитаем издержки на хранение 1 т стали (С^е_хр) за месяц исходя из полученного размера заказа. Они составят 37,95 тыс.руб. (15 кв.м х 21,0 тыс.руб./(мес. х кв.м) х 1 мес. / 8,3 т), где 8,3 т - это среднее количество стали, которое будет иметь место на складе (16,6 / 2).

Уточним оптимальный размер заказа согласно формуле (8):

q_о = √2 х 8 550 х 6 / (37,95 + 0,042 х 8 100) = 16,6 т.

Аналогичным образом были проведены расчеты для остальных месяцев года. Результаты таких расчетов представлены в таблице 2.

Таблица 2

Расчет оптимального размера заказа по месяцам года

Наименование месяца	Величина потребления листовой стали, т	Затраты на хранение 1 т стали за месяц (С^е_хр), тыс.руб./(т х мес.)	Коэффициент эффективности финансовых вложений (Е), за месяц	Расчетный оптимальный размер заказа (q_о), т
Январь	6	37,95	0,042	16,5
Февраль	12	26,82	0,042	23,6
Март	15	24,00	0,042	26,5
Апрель	10	29,43	0,042	21,5
Май	6	37,95	0,042	16,5
Июнь	5	41,55	0,042	15,0
Июль	8	32,85	0,042	19,2
Август	15	24,00	0,042	26,5
Сентябрь	10	29,43	0,042	21,5
Октябрь	5	41,55	0,042	15,0
Ноябрь	4	46,47	0,042	13,3
Декабрь	4	46,47	0,042	13,3

Обратим внимание, что при определении оптимального размера заказа за месяц (см. таблицу 2) не принималась во внимание зависимость расходов на выполнение одного заказа (C^e_o) от величины заказа. Данное обстоятельство объясняется тем, что величина этих затрат зависит не только от размера заказа, но и от имеющихся в наличии автотранспортных агрегатов, которые могут использоваться для транспортировки листовой стали. Так, для транспортировки 15,0 т стали может применяться транспортный агрегат грузоподъемностью 15,0 т. При этом расходы на выполнение одного заказа с помощью данного агрегата, как правило, сопоставимы с расходами на транспортировку 20,0 т стали транспортным агрегатом грузоподъемностью 20,0 т. Между тем следует отметить, что в случаях, когда транспортное средство за один рейс осуществляет доставку товаров нескольких наименований, расходы на выполнение одного заказа (C^e_o) по каждому наименованию товара должны рассчитываться исходя из занимаемой доли грузоподъемности (грузовместимости) транспортного средства.

Анализ полученных результатов свидетельствует о том, что, несмотря на значительные колебания потребления листвой стали в течение года (4-кратные), вариация оптимального размера заказа не превышает 2 раз. Данный факт указывает на то, что оптимальный размер в большинстве случаев может рассчитываться исходя из средних значений потребления материальных запасов за достаточно продолжительный период времени, например, за квартал.

В противном случае, когда наблюдаются многократные колебания спроса (потребления), год целесообразно разбить, например, на 2 (и более) сезона (сезонов), в которых наблюдается минимальная и максимальная величина спроса (потребления). Затем следует определить оптимальный размер заказа для соответствующего сезона и использовать эти величины при оперативной работе по управлению запасами в течение соответствующего сезона.

Расчет оптимального размера мешков с цементом рассмотрим на примере следующей производственной ситуации.

Пример 2

Организация осуществляет розничную и мелкооптовую торговлю цементом марки М-500. Средняя величина рентабельности продаж в организации составляет 3,0 %. В связи с этим организация остро нуждается в свободных денежных средствах. Среднемесячное потребление - 500 мешков. Мешки с цементом (масса нетто 50 кг) доставляются и хранятся на поддонах 1 200 х 1 000 мм грузоподъемностью 2 500 кг.

Закупочная цена - 55,0 тыс.руб. за мешок при размере заказа до 200 мешков, 50 тыс.руб. за мешок - при размере заказа более 200 мешков. Габаритные размеры мешка массой 50 кг (длина/ширина/высота) - 60х495х90 мм. Максимальная высота укладки мешков с цементом - 1,8 м. Издержки, связанные с эксплуатацией 1 кв.м арендуемого склада в течение месяца, составляют 60,0 тыс.руб.

Закупки цемента осуществляются у поставщика, удаленность которого - 30 км. Доставка обеспечивается собственными транспортными средствами грузоподъемностью 2 000, 3 000, 5 000, 8 000 и 10 000 кг, тарифные ставки на внутрихозяйственные грузоперевозки для которых составляют соответственно 1,5; 2,0; 2,3; 2,7 и 3,0 тыс.руб./км. Доставка мешков с цементом может производиться отдельно или параллельно с другими видами товарной продукции.

Рассчитаем оптимальный размер заказа мешков с цементом по формуле (8).

Так как транспортные расходы на выполнение одного заказа (C^e_o), а также затраты на хранение одного мешка с цементом (С^е_хр) зависят от размера заказа, который еще предстоит определить, необходимо в качестве первого приближения интуитивно установить размер заказа.

Принимая во внимание относительно незначительное расстояние транспортировки, интуитивно устанавливаем размер заказа на уровне 40 мешков, тем самым предполагая, что для транспортировки будет использоваться автотранспорт грузоподъемностью 2 000 кг (40 мешков х 50 кг/мешок).

Во-первых, определим транспортные расходы на выполнение одного заказа (C^e_o) по доставке мешков с цементом указанным транспортным средством. Издержки на выполнение одного заказа на расстояние 60 км (туда и обратно) составят 90,0 тыс.руб. (60 км х 1,5 тыс.руб./км).

Во-вторых, определим издержки на хранение 1 мешка с цементом в течение месяца (С^е_хр). С учетом линейных размеров европоддона (1 200х1 000 мм), его грузоподъемности (не более 2 500 кг), линейных размеров мешка с цементом (600х495х90 мм) на одном поддоне можно разместить не более 12 рядов мешков по 4 мешка в каждом ряду плюс 2 мешка на верхнем ряду (50 мешков). Однако исходя из интуитивного размера заказа (2 000 кг) на поддоне будет сформировано 10 рядов мешков с цементом (40 мешков на поддоне). Поддон, площадь которого составляет 1,2 кв.м, с учетом проходов и проездов будет занимать около 2,0 кв.м пола склада. Следовательно, издержки на хранение одного мешка с цементом (С^е_хр) за месяц составят 6,0 тыс.руб. (2,0 кв.м х 60,0 тыс.руб. / (мес. х кв.м) х 1 мес. / 20 мешков), где 20 мешков - это среднее количество мешков на поддоне в течение месяца (q / 2 = 40 / 2).

Исходя из постановки задачи (организация остро нуждается в свободных денежных средствах) коэффициент Е должен приниматься на уровне, близком к максимальному значению (например, 70 % от максимального значения).

Рассчитаем максимальное значение коэффициента Е за период, равный 1 месяцу, по формуле (7). Так, количество оборотов, которые совершают оборотные средства, задействованные в торговле цементом, за год равно 300: (S / (q / 2) х 12 мес. = 500 / 20 х 12 мес., где q / 2 (20 мешков) - средний запас (остаток) на складе мешков с цементом в течение месяца). На основании того, что рентабельность продаж составляет 3 %, получим:

E = 3 % / (12 х 100 %) х 300 = 0,75 1/мес.

Таким образом, принимая величину коэффициента эффективности финансовых вложений (Е) за период времени, равный 1 месяцу, на уровне 0,53 (0,7 х 0,75), определим размер заказа согласно формуле (8):

q_о = √2 х 90 х 500 / (6,0 + 0,53 х 55,0) = 51 мешок.

Полученный расчетный размер заказа (51 мешок) позволяет утверждать, что принятый интуитивно размер заказа на уровне 40 мешков имеет значительное отличие от оптимальной величины (на 27,5 %).

В связи с этим осуществляем второе приближение. Для этого устанавливаем размер заказа с определенным опережением к уровню 51 мешка, принимая в качестве второго приближения размер заказа, равный 100 мешков, тем самым предполагая, что для транспортировки будет использоваться автотранспорт грузоподъемностью 5 000 кг (100 мешков х 50 кг/мешок).

Транспортные расходы на выполнение одного заказа (C^e_o) по доставке мешков с цементом указанным транспортным средством составят 138,0 тыс.руб. (60 км х 2,3 тыс.руб./км).

Пересчитаем издержки на хранение одного мешка с цементом в течение месяца (С^е_хр). С учетом грузовместимости поддона (50 мешков с цементом) на склад поступит 2 поддона. В таком случае издержки на хранение одного мешка с цементом (С^е_хр) за месяц составят 4,8 тыс.руб. (2,0 кв.м / 1 поддон х 2 поддона х 60,0 тыс.руб./(мес. х кв.м) х 1 мес. / 50 мешков, где 50 мешков - это среднее количество мешков на 2 поддонах в течение месяца (q / 2 = 100 / 2)).

Пересчитаем максимальное значение коэффициента Е за период, равный 1 месяцу, по формуле (7). Так, количество оборотов, которые совершают оборотные средства, задействованные в торговле цементом, за год равно 120: (S / (q / 2) х 12 мес. = 500 / 50 х 12 мес., где q / 2 (50 мешков) - средний запас (остаток) на складе мешков с цементом в течение месяца). Исходя из того, что рентабельность продаж составляет 3 %, получим:

E = 3 % / (12 х 100 %) х 120 = 0,31 мес.

Таким образом, принимая величину коэффициента Е за период времени, равный одному месяцу, на уровне 0,21 (0,7 х 0,3), определим размер заказа согласно формуле (8):

q_о = √2 х 138 х 500 / (4,8 + 0,21 х 55,0) = 92 мешка.

Полученный расчетный оптимальный размер заказа (92 мешка) незначительно отличается от размера заказа, принятого в качестве второго приближения (100 мешков).

Следовательно, оптимальный размер заказа мешков с цементом при заданных исходных данных и условии, что цемент будет доставляться отдельно от других видов товаров, составляет около 100 мешков.

Между тем важно знать, как меняется размер заказа, если мешки с цементом доставляются параллельно с другими товарами, а закупка осуществляется со склада одного поставщика.

Например, принимая интуитивно размер заказа на уровне 50 мешков с цементом (масса заказа - 2 500 кг), выбираем в качестве транспортного средства автомобиль грузоподъемностью 5 000 кг, т.е. предусматриваем тот факт, что параллельно с цементом будет доставляться другой товар массой около 2 500 кг.

В этом случае транспортные расходы на выполнение одного заказа (C^e_o) по доставке мешков с цементом указанным транспортным средством будут равны 69,0 тыс.руб. (0,5 х 60 х 2,3 тыс.руб.).

Пересчитаем максимальное значение коэффициента Е за период, равный 1 месяцу, по формуле (7). Так, количество оборотов, которые совершают оборотные средства, задействованные в торговле цементом, за год равно 240: (S / (q / 2) х 12 мес. = 500 / 25 х 12 мес., где q / 2 (25 мешков) - средний запас (остаток) на складе мешков с цементом в течение месяца). На основании того, что рентабельность продаж составляет 3 %, получим:

Е = 3 % / 12 х 100 % х 240 = 0,6 1/мес.

Таким образом, принимая величину коэффициента эффективности финансовых вложений (Е) за период времени, равный 1 месяцу, на уровне 0,42 (0,7 х 0,6), определим размер заказа согласно формуле (8):

q_о = √2 х 69 х 500 / (4,8 + 0,42 х 55,0) = 50 мешков.

Полученный расчетный оптимальный размер заказа (50 мешков) не отличается от принятого в качестве первого приближения (50 мешков). Поэтому принятый размер заказа на уровне 50 мешков при условии, что цемент будет доставляться автомобилем грузоподъемностью 5 000 кг параллельно с другими товарами, является экономически оправданным решением.

Таким образом, доставка цемента посредством применения транспортных средств большой и особо большой грузоподъемности параллельно с другими товарами позволяет сократить размер заказа мешков с цементом на 50 % и более по сравнению с ситуацией, когда цемент доставляется отдельно от других видов товаров.

Между тем сокращение размера заказа имеет определенное ограничение. Как отмечалось выше, его размер не должен быть меньше величины потребления за время выполнения заказа. Так, в нашем примере, время выполнения заказа обычно не превышает двух дней. В этой связи, величина потребления за данный период составит в среднем 46 мешков с цементом (500 мешков/мес. / 22 раб. дня х 2 дня). Следовательно, с организационной точки зрения, размер заказа не должен быть меньше 46 мешков с цементом.

Расчет оптимального размера при стеллажном размещении запасов рассмотрим на примере следующей производственной ситуации.

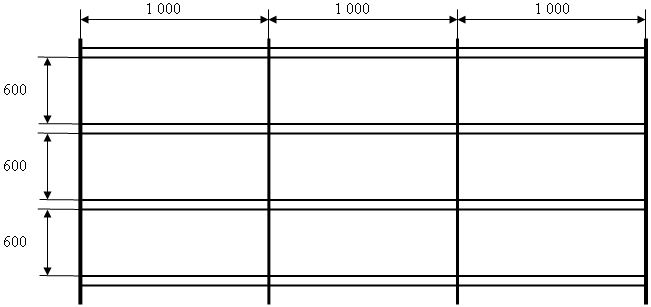
Пример 3

Организация осуществляет розничную и мелкооптовую торговлю бумагой офисной формата А-4 в пачках по 500 листов. Пачки бумаги доставляются и хранятся в коробках, вмещающих 5 пачек. Закупочная цена - 45,0 тыс.руб. за пачку при размере заказа до 200 пачек, 40 тыс.руб. за пачку - при размере заказа от 200 до 500 пачек и 37 тыс.руб. за пачку - при размере заказа более 500 пачек. Среднемесячное потребление бумаги - 1 000 пачек. Габаритные размеры коробки (длина/ширина/высота) - 300х220х275 мм. Масса брутто одной коробки - 12,5 кг. Коробки хранятся в стеллажах СТ-031 (см. рисунок 2).

Рисунок 2

Размеры стеллажа СТ-031, мм

Максимальная нагрузка на полку стеллажа - 200 кг. Издержки, связанные с эксплуатацией 1 кв.м арендуемого склада в течение месяца, составляют 50,0 тыс.руб.

Закупки бумаги осуществляются у поставщика, удаленность которого - 40 км. Доставка обеспечивается собственными транспортными средствами грузоподъемностью 1 000, 2 000 и 3 000 кг, тарифные ставки на внутрихозяйственные грузоперевозки для которых составляют соответственно 1,5, 2,2 и 2,5 тыс.руб./км. Доставка бумаги может производиться отдельно или параллельно с другими видами товарной продукции. Средняя рентабельность продаж имеет достаточно высокое значение. Это обуславливает тот факт, что организация не нуждается в дополнительных (свободных) денежных средствах.

Рассчитаем оптимальный размер заказа бумаги по формуле (8).

Принимая во внимание относительно незначительное расстояние транспортировки, интуитивно устанавливаем размер заказа на уровне 100 пачек (20 коробок). Масса заказа - 250 кг (12,5 кг / 1 коробка х 20 коробок) обуславливает применение транспортного средства грузоподъемностью 1 000 кг. При этом предусматривается, что параллельно с бумагой у поставщика будет заказываться другой товар до полной загрузки транспортного средства.

Во-первых, определим транспортные расходы на выполнение одного заказа (C^e_o) по доставке бумаги. Издержки на выполнение одного заказа на расстояние 80 км (туда и обратно) составят 30,0 тыс.руб. (250 / 1 000 х 80 км х 1,5 тыс.руб./км).

Во-вторых, определим издержки на хранение 1 пачки бумаги в течение месяца (С^е_хр). Линейные размеры одной полки стеллажа СТ-031 позволяют разместить на ней 8 коробок бумаги, или соответственно 40 пачек в коробках. Исходя из рисунка 3 можно утверждать, что одна полка стеллажа занимает лишь 0,075 кв.м (3 м х 0,3 м / 12 полок), а с учетом проходов и проездов - около 0,1 кв.м. Следовательно, издержки на хранение 1 пачки бумаги (С^е_хр) за месяц составят 0,25 тыс.руб. (0,1 кв.м х 50,0 тыс.руб./(мес. х кв.м) х 1 мес. / 20 пачек, где 20 пачек - это среднее количество пачек бумаги на одной полке стеллажа в течение месяца (q / 2 = 40 / 2)).

С учетом исходной информации (организация не нуждается в дополнительных (свободных) денежных средствах) Принимая величину коэффициента эффективности финансовых вложений (Е) за период времени, равный 1 месяцу, на уровне 0,05 (т.е. предполагая возможность дальнейшего но незначительного наращивания объемов торговой деятельности), определим размер заказа согласно формуле (8):

_____________________ ____________________________

q_o = √2 х C^e_o х S / (С^е_хр +E х P) = √2 х 30 х 1 000 / (0,25 + 0,05 х 45,0) = 155 пачек.

Полученный расчетный размер заказа (155 пачек) позволяет утверждать, что принятый интуитивно размер заказа на уровне 100 пачек имеет значительное отличие от оптимальной величины.

В связи с этим осуществляем второе приближение. Для этого устанавливаем размер заказа с определенным опережением к уровню 155 пачек, принимая в качестве второго приближения размер заказа, равный 250 пачек, или 50 коробок. Масса заказа, составляющая 625 кг (12,5 кг / 1 коробка х 50 коробок), обуславливает применение транспортного средства грузоподъемностью 1 000 кг. При этом также предусматривается, что параллельно с бумагой у поставщика будет заказываться другой товар до полной загрузки транспортного средства.

Определим транспортные расходы на выполнение одного заказа (C^e_o) по доставке бумаги. Издержки на выполнение одного заказа на расстояние 80 км (туда и обратно) составят 75,0 тыс.руб. (625 / 1 000 х 80 км х 1,5 тыс.руб./км).

Издержки на хранение одной пачки бумаги в течение месяца (С^е_хр) останутся прежними (0,25 тыс.руб.).

В этом случае размер заказа согласно формуле (8) составит:

q_o = √2 х 75 х 1 000 / (0,25 + 0,05 х 40,0) = 258 пачек.

Полученный расчетный оптимальный размер заказа (258 пачек) отличается всего на 3,2 % от размера заказа, принятого в качестве второго приближения.

Следовательно, оптимальный размер заказа бумаги при заданных исходных данных и условии, что бумага будет доставляться параллельно с другими видами товаров, составляет около 250 пачек, или 50 коробок.

Заключение

Таким образом, анализ рассмотренных примеров по определению оптимального размера заказов материальных запасов при различных способах их размещения на складе позволяет сделать следующие выводы и рекомендации:

• размер заказа по отдельным наименованиям материальных запасов во многом зависит от способа размещения товара на складе;

• доставку заказа определенного наименования запаса в большинстве случаев целесообразно осуществлять параллельно с другими товарами до полной загрузки транспортного средства;

• для товаров (упаковок товаров), отличающихся незначительными габаритами и небольшой объемной массой, предпочтение следует отдавать стеллажному способу хранения.

30.03.2012 г.

Петр Дроздов, кандидат экономических наук, доцент Белорусского государственного аграрного технического университета